Arbitrarily Scalable Environment Generators via Neural Cellular Automata

Yulun Zhang, Matthew C. Fontaine, Varun Bhatt, Stefanos Nikolaidis, Jiaoyang Li

October 2023

Abstract

We study the problem of generating arbitrarily large environments to improve the throughput of multi-robot systems. Prior work proposes Quality Diversity (QD) algorithms as an effective method for optimizing the environments of automated warehouses. However, these approaches optimize only relatively small environments, falling short when it comes to replicating real-world warehouse sizes. The challenge arises from the exponential increase in the search space as the environment size increases. Additionally, the previous methods have only been tested with up to 350 robots in simulations, while practical warehouses could host thousands of robots. In this paper, instead of optimizing environments, we propose to optimize Neural Cellular Automata (NCA) environment generators via QD algorithms. We train a collection of NCA generators with QD algorithms in small environments and then generate arbitrarily large environments from the generators at test time. We show that NCA environment generators maintain consistent, regularized patterns regardless of environment size, significantly enhancing the scalability of multi-robot systems in two different domains with up to 2,350 robots. Additionally, we demonstrate that our method scales a single-agent reinforcement learning policy to arbitrarily large environments with similar patterns.

Type

Conference paper

Publication

In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), December 10–16, New Orleans, LA, USA

Introduction

Our previous work [1] formulates the environment optimization problem as a Quality Diversity (QD) optimization problem and optimizes the environments by searching for combination of tiles. The optimized environments have much higher throughput and are more scalable than human-designed ones. However, with this method, the search space of the QD algorithm grows exponentially with the size of the environment.

Therefore, instead of optimizing the environments directly, this paper proposes to optimize Neural Cellular Automata (NCA) environment generators via QD algorithms. We show that NCA-generated environments maintain consistent, regularized patterns regardless of environment size, significantly enhancing the scalability of multi-robot systems.

Approach Overview

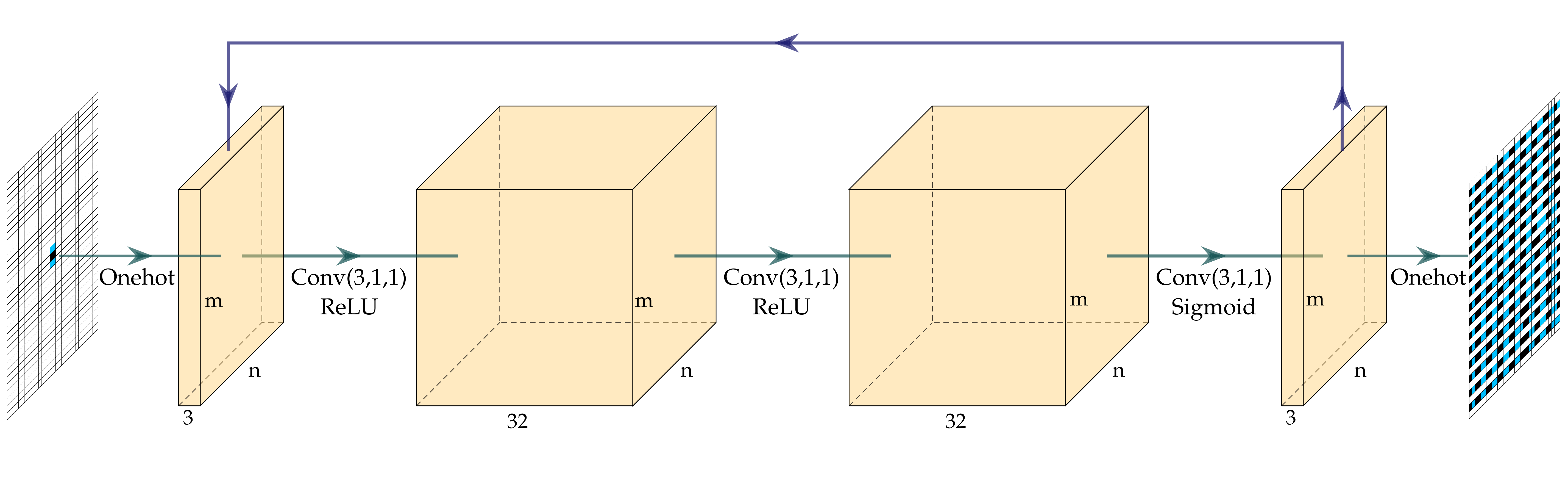
We extend previous works [1,2] to use CMA-MAE [3] to search for a diverse collection of NCA generators with the objective and diversity measures computed from an agent-based simulator that runs domain-specific simulations in generated environments. Figure 1 provides an overview of our method. We start by sampling a batch of $b$ parameter vectors $\boldsymbol{\theta}$ from a multivariate Gaussian distribution, which form $b$ NCA generators. Each NCA generator then generates one environment from a fixed initial environment, resulting in $b$ environments. Figure 2 shows the architecture of the NCA generator.

We then repair the environments using a Mixed Integer Linear Programming (MILP) solver to enforce domain-specific constraints. After getting the repaired environments, we evaluate each of them by running an agent-based simulator for $N_e$ times, each with $T$ timesteps, and compute the average objective and measures. We add the evaluated environments and their corresponding NCA generators to both the optimization archive and the result archive. Finally, we update the parameters of the multivariate Gaussian distribution (i.e., $\mu$ and $\Sigma$) and sample a new batch of parameter vectors, starting a new iteration.

**Figure 2:** NCA generator architecture. It is a convolutional neural network (CNN) with 3 convolutional layers of kernel size 3 × 3 followed by ReLU or sigmoid activations.

Results

NCA-generated Environments

Figure 3 shows the NCA-generated environments of different sizes, showing that the trained NCA generators can generate environments of different sizes with consistent regularized patterns. Figure 4 shows an example NCA generation process of 200 iterations.

Figure 4: Example NCA generation process for environment of size 101 $\times$ 102.

Scalability

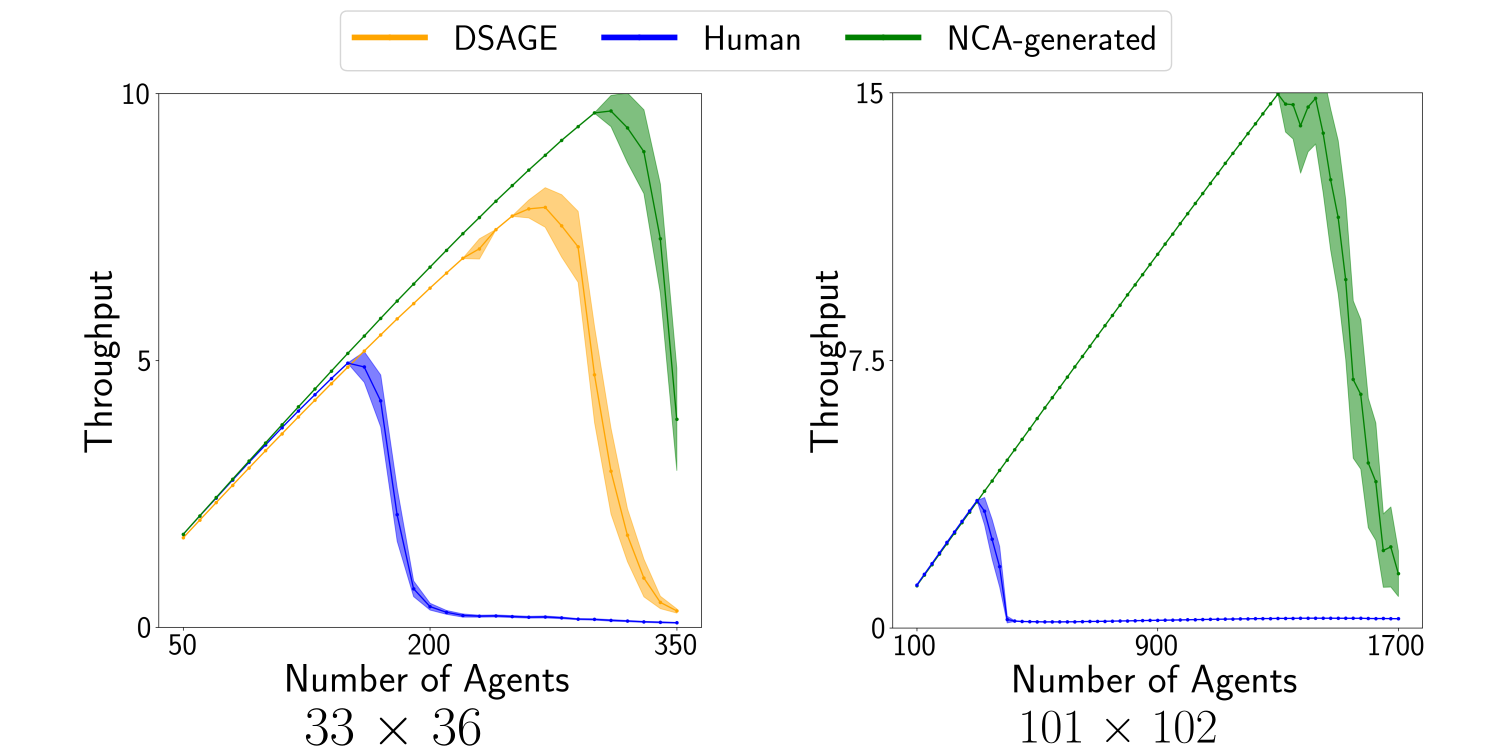
We then analyze the scalability of the environments by running simulations with varying numbers of agents and show the throughput. We compare our NCA-generated environments with those optimized by DSAGE [1], the state-of-the-art environment optimization algorithm, and human-designed ones. Figure 5 shows the result. Our NCA-generated environments have higher throughput than the baseline environments with an increasingly larger gap with more agents.

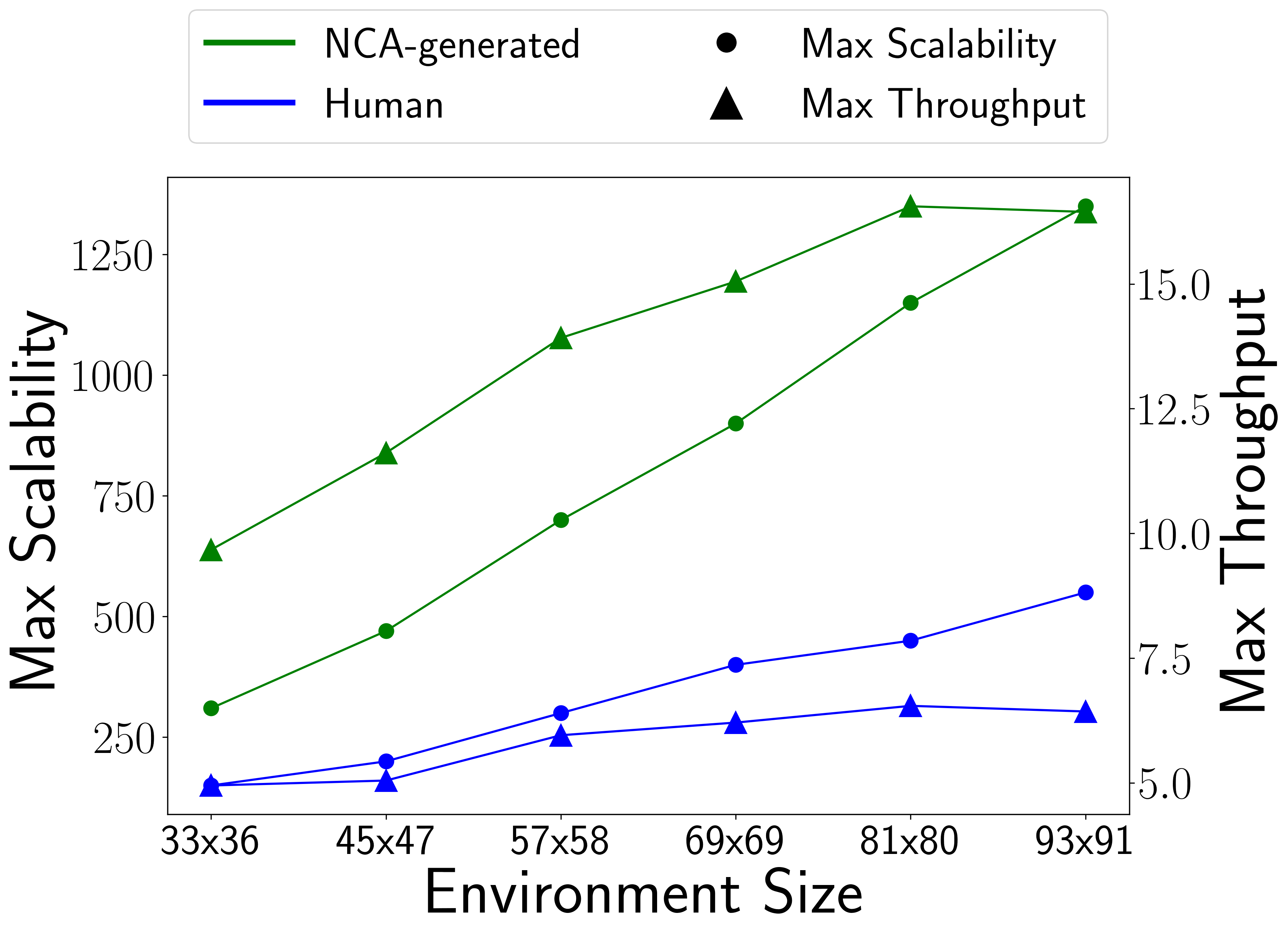
**Figure 5:** Throughput with an increasing number of agents in environments of size 33 $\times$ 36 and 101 $\times$ 102.

We further analyze the scalability of the NCA-generated environments in other sizes. Figure 6 shows the result. The y-axis illustrates two metrics: maximum mean throughput over 50 simulations (right) and the maximum scalability, defined as the agent count at this maximum (left).

**Figure 6:** Scalability of NCA-generated environments.

Scaling Single-Agent RL Policy

We also train NCA generators for a single-agent maze domain and generate environments with consistent patterns with different sizes (18x18 and 66x66). In this domain, we show that it is possible to scale a single-agent RL policy to larger environments with similar regularized patterns. We run an RL agent (a trained ACCEL [4] agent) trained in 18x18 environments in the 66x66 one for 100 times, resulting in a 93% success rate. The high success rate comes from the fact that the similar local observation space of the RL policy enables the agent to make the correct local decision and eventually arrive at the goal. Figure 7 shows the generated environments and videos of the agent solving the two environments.

18 $\times$ 18

66 $\times$ 66

Figure 7: NCA-generated maze environments which are solved by an RL agent trained in 18 $\times$ 18 environments.

References

[1] Yulun Zhang, Matthew C. Fontaine, Varun Bhatt, Stefanos Nikolaidis, and Jiaoyang Li. Multi-robot coordination and layout design for automated warehousing. In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI), pages 5503–5511, 2023.

[2] Sam Earle, Justin Snider, Matthew C. Fontaine, Stefanos Nikolaidis, and Julian Togelius. Illuminating diverse neural cellular automata for level generation. In Proceedings of the Genetic and Evolutionary Computation Conference (GECCO), pages 68–76, 2022.

[3] Matthew Fontaine and Stefanos Nikolaidis. Covariance matrix adaptation map-annealing. In Proceedings of the Genetic and Evolutionary Computation Conference (GECCO), pages 456–465, 2023.

[4] Jack Parker-Holder, Minqi Jiang, Michael Dennis, Mikayel Samvelyan, Jakob Foerster, Edward Grefenstette, and Tim Rocktäschel. Evolving curricula with regret-based environment design. In Proceedings of the International Conference on Machine Learning (ICML), pages 17473–17498, 2022.